In order to better understand neural networks, I wanted to see one implemented with a minimal amount of code. I quickly found a neural network in 11 lines of Python. It’s a great little piece of code that learns the XOR function and shows the backpropagation in action. I felt however, that I needed a slightly more complex example - a neural net that could recognize handwritten digits from the MNIST dataset:

Michael Nielsen’s great book on neural networks is built upon just this classification problem, but the simplest implementation is 74 lines of code (without the comments). So I took that code and refactored it down to 25 lines (source):

import numpy as np
import mnist

def feed_forward(X, weights):
    a = [X]
    for w in weights:
        a.append(np.maximum(a[-1].dot(w),0))
    return a

def grads(X, Y, weights):
    grads = np.empty_like(weights)
    a = feed_forward(X, weights)
    delta = a[-1] - Y
    grads[-1] = a[-2].T.dot(delta)
    for i in xrange(len(a)-2, 0, -1):
        delta = (a[i] > 0) * delta.dot(weights[i].T)
        grads[i-1] = a[i-1].T.dot(delta)
    return grads / len(X)

trX, trY, teX, teY = mnist.load_data()
weights = [np.random.randn(*w) * 0.1 for w in [(784, 100), (100, 10)]]
num_epochs, batch_size, learn_rate = 30, 20, 0.1

for i in xrange(num_epochs):
    for j in xrange(0, len(trX), batch_size):
        X, Y = trX[j:j+batch_size], trY[j:j+batch_size]
        weights -= learn_rate * grads(X, Y, weights)
    prediction = np.argmax(feed_forward(teX, weights)[-1], axis=1)
    print i, np.mean(prediction == np.argmax(teY, axis=1))

If you run this code, you will get to about 97.8% accuracy on the test set.

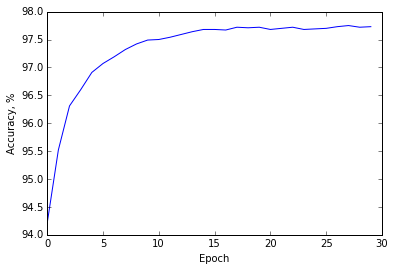
The algorithm is practically the same as the original implementation. The net has one hidden layer with 100 neurons and uses mini batch gradient descent to learn the weights. It has two dependencies - numpy, which handles vector and matrix operations, and mnist which is a simple script that downloads the MNIST data and loads it to memory.

The major difference is that instead of loops I use matrix operations, which means you can process the entire mini batch as a matrix instead of iterating over each training example. As a result, the training is about 5 times faster than the original code, while you can still see what’s going on under the hood. I changed the activation function from sigmoid to ReLU, which is just f(x) = max(0, x) and its derivative is as simple as x > 0 (applied element-wise). I’ve also dropped the bias terms because in this problem they do not considerably improve accuracy.

Implementation with a high-level ML library

Once we understand how backpropagation works, we can hide the complexity by using a machine learning library. So I implemented the exact same network as above using Theano, TensorFlow, Keras and Torch - see here.